موضوع ریاضی نهم فصل اول مجموعه ها و احتمال است. این فصل شامل 4 درس است با نگرش همراه باشید:
1.معرفی مجموعه ها
2.مجموعه های برابر و نمایش مجموعه ها
3.اجتماع،اشتراک و تفاضل مجموعه ها
4.مجموعه ها و احتمال
مجموعه ها در ریاضی نهم
در درس اول این درس راجع به اینکه تعریف مجموعه چیست و مجموعه چه ویژگی هایی دارد صحبت میشود.
مجموعه چیست؟ از عبارت مجموعه برای بیان و نمایش دسته ای از اشیای مشخص و متمایز استفاده میکنیم. یعنی اینکه دسته ای از اشیا که عضویت آن ها در مجموعه کاملا معین باشد و این اعضا غیرتکراری باشند.
دو نکته را در نوشتن مجموعه باید توجه داشت : اول اینکه ترتیب نوشتن اعضای مجموعه مهم نیست و با جابجایی اعضای مجموعه ،مجموعه ی جدیدی تشکیل نمیشود. دوم اینکه با تکرار یک عضو هم مجموعه جدیدی ساخته نمیشود ، بنابراین اگر در یک مجموعه یک عضو دو بار یا بیشتر تکرار شده باشد آن را یکی حساب میکنیم.
A = {2,5,5} برابر است با A = {2,5} و همچنین A = {2,3,5} برابر است با A = {5,2,3}
برای نشان دادن عضو بودن در مجموعه در ریاضی از این علامت استفاده میکنیم ∈ و عضو نبودن در مجموعه در ریاضی از این علامت ∉ استفاده میکنیم.
بنابراین اگر مجموعه A={1,2,3,4} در نظر بگیریم . 1∈A یعنی 1عضو مجموعه A است . و 6∉A یعنی 6 عضو مجموعه A نیست.
مجموعه را می شود با نمودار ون که به صورت منحنی یا خط های شکسته بسته است نمایش داد.
به مجموعه ای که عضوی نداشته باشد،مجموعه تهی میگویند و آن را با این علامت نشان می دهند. ∅یا {} .
مجموعه های برابر و نمایش مجموعه ها
مجموعه های برابر به مجموعه هایی گفته می شود که عضو های آن ها دقیقا یکسان باشند و مثلا هر عضو مجموعه A در مجموعه B نیز باشد. در این صورت میگوییم که مجموعه A و B با هم برابر هستند و آن را این گونه A = B نشان می دهیم.
اگر حتی یک عضو از مجموعه A در مجموعه B نباشد و یا برعکس ،در این صورت می گوییم مجموعه A و B با هم برابر نیستند و آن را اینگونه A ≠ B نشان میدهیم.
زیرمجموعه در ریاضی
اگر دو مجموعه A و C را در نظر بگیریم. اگر هر عضو از مجموعه A در مجموعه C باشد و مجموعه C بزرگتراز مجموعه A باشد و کامل آن را در بر بگیرد. میگوییم که مجموعه A زیر مجموعه C است و آن را این گونه A ⊆ D نشان می دهیم.
ولی اگر بتوانیم حتی یک عضو را در مجموعه A پیدا کنیم که در مجموعه C نباشد میگوییم مجموعه A
زیرمجموعه Cنیست و آن را با این علامت تصویر6 نشان می دهیم.
- هر مجموعه زیر مجموعه خودش است.
- مجموعه تهی زیر مجموعه هرمجموعه دلخواهی است.
نمایش مجموعه های اعداد
نمای مجموعه به 3 صورت امکان پذیر است: نمایش عضوها،نمودار ون و نمادهای ریاضی.
نمایش مجموعه ی اعداد با نماد ریاضی: برای این کار باید از نمادهای ریاضی برای نشان دادن مجموعه استفاده کنیم برای مثال: مجموعه عدد های طبیعی زوج را به این صورت نشان میدهیم E={2k|k∈N}
و این طور میخوانیم که مجموعه E برابراست با مجموعه ای از اعداد به شکل 2k به طوری که k متعلق به اعداد طبیعی است.
2k به معنای اعداد زوج است.
ǀ به معنای به طوری که است.
N به معنای اعداد طبیعی است.
- مجموعه اعداد طبیعی (N) زیر مجموعه اعداد حسابی (W) است و هر دوی این مجموعه ها زیر مجموعه ی اعداد صحیح (Z) هستند. N⊆W⊆Z
اجتماع، اشتراک، تفاضل مجموعه ها
اشتراک دو مجموعه :مجموعه ای که همه عضو های آن هم عضو مجموعه A باشند و هم عضو مجموعه B باشند که آن را با این علامت A∩B نشان می دهیم
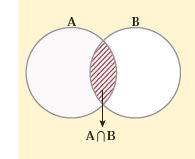
اجتماع دو مجموعه : اجتماع دو مجموعه A و B ، مجموعه ای است شامل همه عضوهایی که حداقل در یکی ازدو مجموعه باشند. یعنی تمام عضوهای مجموعه A به علاوه تمام عضو های مجموعه B و آن را با علامت A∪B نشان می دهیم.
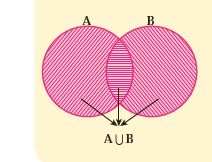
تفاضل دو مجموعه: مجموعه ای است که شامل همه عضو های مجموعه اول باشد به جز آن هایی که با مجموعه دوم مشترکند. یعنی مجموعه A-B (A منهای B) مجموعه ای است شامل همه عضو هایی که عضو مجموعه A هستند اما عضو مجموعه B نیستند که آن را با علامت A-B نشان می دهیم.
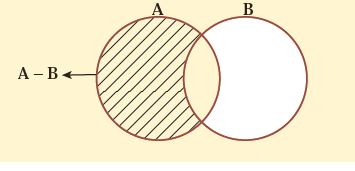
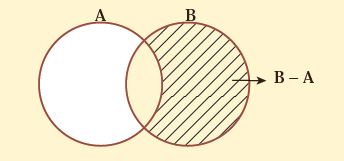
- تعداد عضو های هر مجموعه را با حرف n نشان میدهیم. مثلا اگر بخواهیم بگوییم تعداد اعضای مجموعه B ، k عدد است آن را به این صورت نشان میدهیم: n(B)=k
B={1,4,7} در این صورت n(B)=3
احتمال در ریاضی نهم
تعریف احتمال: احتمال انجام شدن یک اتفاق برابر است با تعداد حالت های مد نظر تقسیم بر تعداد حالت های کل . که این فرمول در ریاضی به این صورت نوشته می شود:
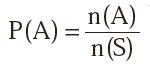
![]()
